Derivation of 3rd-order Birch-Murnaghan equation of state
The concept of the 3rd-order Birch-Murnaghan equation of state (BM3-EOS) is almost the same as that of the 2nd-order Birch-Murnaghan equation of state (BM2-EOS).
Difference is that change in Helmholtz free energy, F, is expanded not to the 2nd-order (BM2 Eq. 3) but to the 3rd-order the finite strain f (BM2 Eq. 2):
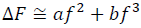
(1)
By differentiating Eq. (1) by V with the relations between P and F (BM2 Eq. 1), we have P as:
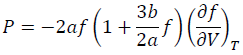
(2)
According to the calculation shown in the separate page, the factor 3b/2a is:
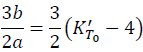
(3)
By substituting the definition of the finite strain (BM2 Eq. 2), its volume derivative (BM2 Eq. 6), the parameter "a" (BM2 Eq. 5), and the parameter "3b/2a" (Eq. 3) into Eq. (2), we have:
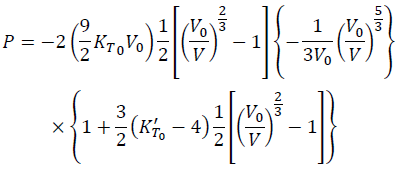
(4)
By simplifying Eq. (4), we have BM3-EOS:
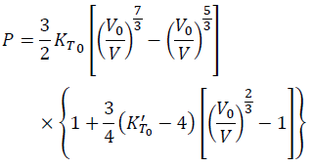
(5)
As well as BM2-EOS, BM3-EOS is obtained based on the definition of finite strain. Hence, appropriateness of the definition of the finite strain is responsible for this EOS.
BM3-EOS becomes identical to BM2-EOS if KT0' = 4. Therefore, BM-EOS can be justified (or, is useful for our purpose), if the matters of our interest have KT0' ~ 4. As is shown in the table (not yet made), KT0' of many mantle minerals are around 4.
Poirier [2000] provided an excellent explanation about the Birch-Murnaghan equation of state (p. 66-74, Section 4.3). I imagine, however, that many current high-pressure workers need a plainer explanation. Actually, it is not easy to derive the third-order Birch-Murnaghan equation of state only based on what is written in Poirier [2000].
I made the present page to provide a mathematically easier explanation by referring to this book and also by referring to Section 6.2 in Anderson [1995].
Reference:
Anderson, O. L., Equations of state of solids for geophysics and ceramic science, Oxford University Press, New Yourk, pp. 405, 1995
Poirier, J. P. Introduction to the physics of the Earth's Interior 2nd edition, Cambridge University Press, Cambridge, pp. 312, 2000.
