Why Eulerian Finite Strain?
- EOS by Lagrangian finite strain
They say that the Eulerian finite strain is necessary and useful to consider HP compression and construct proper equation of states [Wiki].
However, it is not clear (at least, it was absolutely unclear for me.) how useful the Eulerian finite strain is.
Therefore, let me argue in this page why the Eulerian strain is useful.
Two schemes to describe strains
Eulerian scheme
The unstrained state before compression are expressed by the coordinates in the strained state after compression.
Lagrangian scheme
The strained state after compression are expressed by the coordinates in the unstrained state before compression.
We adopt the Eulerian scheme. Then, why was the Lagrangian scheme discarded? In order to answer this question, let me construct an equation of state in the Lagrangian scheme.
Lagrangian finite strain
Let us consider a cube with an edge length of X0 and volume V0 = X03 in an unstrained state. This cube is compressed to an edge length of X and volume V = X3 (See the figure below). The change of the edge length is expressed by u.
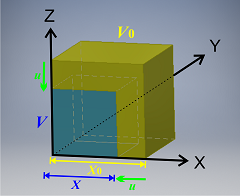
Namely,

(1)
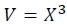
(2)

(3)
This setting is identical to the case of the Eulerian scheme.
As is mentioned above, we argue change in square of the edge length by compression. However, unlike the Eulerian scheme, we express it not by X but by X0 in the Lagrangian scheme.
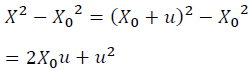
(4)
Similar to the Eulerian scheme, we have a proportionality between X0 and u.
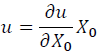
(5)
Then we have:
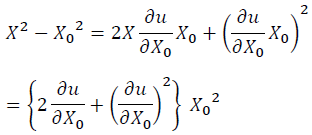
(6)
We define the Lagrangian finite strain as:

(7)
Similar to the Eulerian scheme,
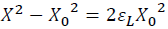
(8)
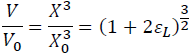
(9)
The Lagrangian finite strain is expressed by the volume ratio as:
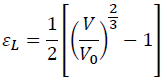
(10)
We have a convenient Lagrangian finite strain as:

(11)
2nd-order Lagrangian EOS
Then, let us construct the 2nd-order equation of state based on the Lagrangian finite strain, which is called the Lagrangian EOS here.
Like the 2nd-order Birch-Murnaghan EOS (Eulerian EOS), we first assume that the Helmholtz free energy increases with square of the Lagrangian finite strain as:

(12)
where fL is the Lagrangian finite strain.
The formula of P in the Lagrangian scheme is identical to the Eulerian scheme.
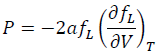
(13)
However, the V derivative of the finite strain is different:
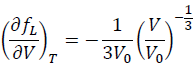
(14)
By substituting Eqs. (11) and (14) into Eq. (13), we have
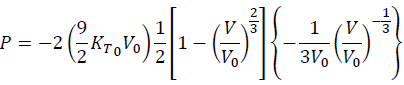
(15)
Then, we have the 2nd-order Lagrangian equation of state as:
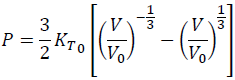
(16)
Let us compare the Eulerian (2nd-order Birch-Murnaghan) and Lagrangian equations of state using MgSiO3 bridgimanite as a working matter. Siogeikin et al. [2004] obtained KS0 = 253(3) GPa by Brillouin scattering. Here we assume KT0 = KS0. Tange et al. [2012] measured volumes of MgSiO3 bridgmanite at pressures of 28 to 98 GPa and ambient temperature. Pressures obtained by the Eulerian (BM Eq. 8) and Lagrangian (Eq. 16) EOS's based on the above KT0. are compared with MgO pressures in the diagram below.
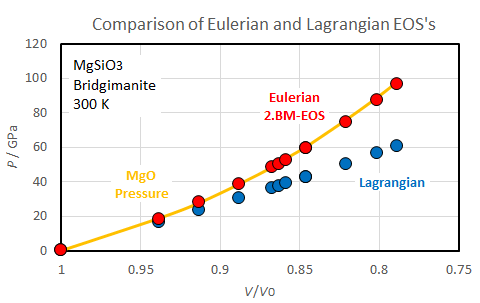
Fig. 1.
This diagram demonstrates that, although the Eulerian EOS (2. BM-EOS) gives correct pressures only with knowledge of KT0, the Lagrangian EOS significantly underestimates pressures. In other words, the Eulerian EOS contains the property that matter becomes less compressible at high pressures, whereas the Lagrangian EOS does not. The reason for this difference is that the V derivative of the finite strain increases with inverse proportion to the 5/3 power of V in the Eulerian scheme (BM2 Eq. 6), whereas it increases with inverse proportion to only the 1/3 power of V in the Lagrangian scheme (this page, Eq. 14). This fact is also seen by their volume exponents in the two EOS's (BM2 Eq. 8 and this page Eq. 16). The exponents are more close to 0 in the Lagrangian scheme (-1/3 and 1/3) than the Eulerian scheme (7/3 and 5/3).
Let us discuss further more why the Eulerian pressure increases more rapidly than the Lagrangian pressure. As is shown in Eq. (3), the pressure is proportional to the product of finite strain and its volume derivative. Fig. 2 shows increase of the Eulerian and Lagrangian finite strains with volume decrease.
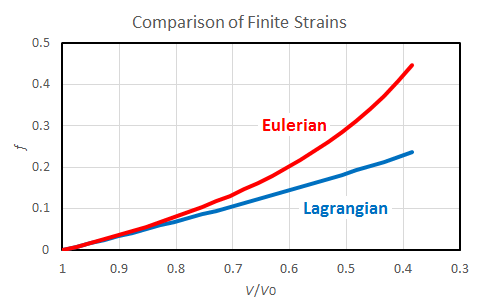
Fig. 2
As is seen, the Eulerian strain more rapidly increases than the Lagrangian strain.
Why like this? Eulerian and Lagrangian finite strains are both differences between the 2/3 power of volume ratio and unity. In the case of Eulerian strain, the ratio is the unstrained volume to the strained volume, and therefore the Eulerian strain can be infinitely large with decreasing volume, whereas the Lagrangian strain is limited to unity.
However, the more essential reason is the volume derivatives of the finite strain, which are shown in Fig. 3.
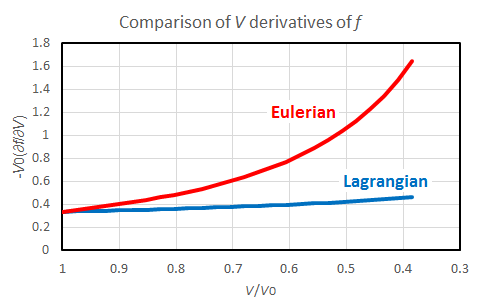
Fig. 3
The volume derivative of the Eulerian strain dramatically increases with volume decrease, whereas that of the Lagrangian strain remains nearly constant. For these reasons, the Eulerian pressure increases more greatly than the Lagrangian pressure.
3rd-order Lagrangian EOS
Next, let us construct the 3rd-order Lagrangian EOS. Just like the 3rd-order Eulerian EOS, increase in Helmholtz free energy is expanded into the third power of fL as:
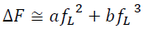
(17)
The differentiation of Eq (17) by V leads to pressure:
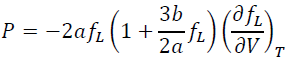
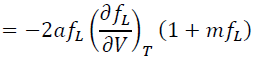
(18)
By differentiating Eq. (14), the second V derivative of fL is given by

(19)
Unlike the Eulerian scheme, the coefficient of the right side does not contain the factor of 5.
At P = 0, we have:
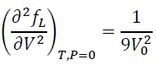
(20)
By differentiating Eq. (18) by V twice, we have the same equation with Eq. (10) in the Eulerian scheme. Eq. (3) in the derivation of the parameter "a" in the BM2.-EOS and Eq. (20) is substituted into this equation, and we have:
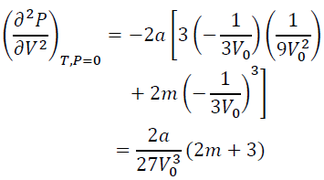
(21)
In the Eulerian scheme, the constant term in the bracket is not 3 but 15.
The second V derivative of P at P = 0 is:
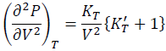
(22)
By equating Eq. (21) and (22), and substituting Eq (5) in the BM2-EOS page into it, we have:
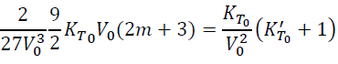
(23)
By simplifying Eq. (23), we have
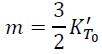
(24)
Unlike the Eulerian scheme, Eq. (24) has no constant term of -4.
In the exactly same way as the Eulerian scheme, we have the 3rd-order EOS in the Lagrangian scheme:
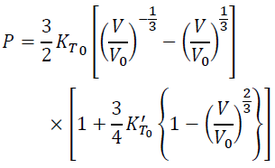
(25)
One of the important difference of the Lagrangian EOS from the 3rd-order Eulerian EOS is absence of constant term of -4 to KT0'. This means that the 3rd-order Lagrangian EOS becomes equivalent to the 2nd-order EOS (Eq. 16) when KT0' = 0. In the case of the Eulerian scheme, the 3rd-order BM-EOS becomes equivalent to the 2nd-order BM-EOS when KT0' = 4. Thus, the 2nd-order Lagrangian EOS does not contain the property that matters become less compressible by compression in contrast to the Eulerian EOS. This is the reason why the 2nd-order Lagrangian EOS is rather straight in the (V/V0)-P space, as is shown in Fig. 1.
Let us compare the 3rd-order EOS in the Eulerian and Lagrangian schemes (Fig. 2). Let us set KT0 = 254 GPa and KT0' = 4.
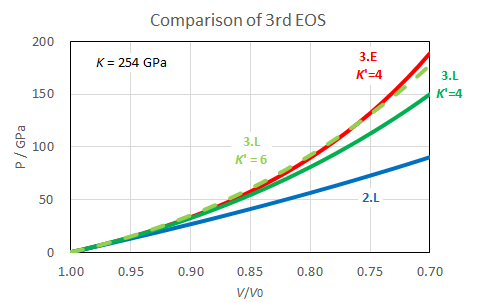
Fig. 4
3.E: 3rd-order Eulerian EOS
3.L: 3rd-order Lagrangian EOS
2.L: 2nd-order Lagrangian EOS
The 3rd-order Lagrangian EOS becomes less compressible especially at high compression than the 2nd-order Lagrangian EOS. However, it is still more compressible than the 3rd-order Eulerian EOS. In order that the Lagrangian EOS has similar (V/V0)-P relations with the Eulerian EOS, KT0' should be around 6. We can imagine that the EOS's in these two schemes become more similar at higher order.
The purpose of EOS in geophysics is to make it possible to evaluate density at high pressures with a small number of information. The fantastic point of the Birch-Murnaghan EOS is that we can estimate density of matter with high accuracy only by KT0! If we adopt the Lagrangian scheme, we cannot properly evaluate density at HP, even though we know both of KT0 and KT0'.
It is suggested that the Eulerian strain is more reasonable than the Lagrangian strain due to the following reason. As V goes to zero, F must go to infinity. As V goes to zero, the Eulerian strain goes to infinity, and therefore F goes to infinity. On the other hand, the Lagrangian strain goes to unity only, and F does not go to infinity.
It seems that the arguments in this page were issues in the early 20th century or even earlier. I do not find this kind of argument in any current literature. Therefore, I am not sure whether the argument in this page is correct or not. If you find any problem in this page, please let me know it.
