Isothermal equation of state
Although high T generally increases V of matters, compression by high P is more significant for considering the Earth's interior. Therefore, we first discuss compression at a constant T, namely, the isothermal EOS.
In thermodynamics, pressure (P) is defined as volume (V) derivative of Helmholtz free energy (F). Namely,
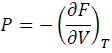
(1)
In this page, we first enumerate isothermal EOS that appear in articles of solid geophysics.
Frequently used isothermal EOS
The simplest EOS is obtained from the definition of the isothermal bulk modulus [Wiki], KT as:
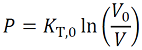
(2)
where V0 is the volume at P = 0 and KT,0 is the isothermal bulk modulus at P = 0. However, KT is not constant but increases with P. By assuming the constant increasing rate of KT with P, we have the Murnaghan's EOS:
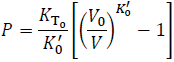
(3)
The most frequently used EOS at constant T in Study of the Earth's Interior is the: 3rd-order Birch-Murnaghan EOS [Wiki] (BM3-EOS):
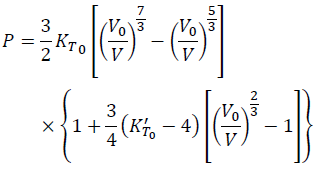
(4)
The lower order of Birch-Murnaghan EOS, namely, 2nd-order Birch-Murnaghan EOS [Wiki] (BM2-EOS) is:
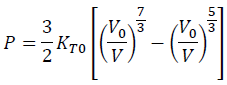
(5)
BM3-EOS becomes identical to BM2-EOS when KT0' = 4. The relation KT0' = 4 is the case in many kinds of materials.
Recently, the Vinet EOS (V-EOS) is also used.
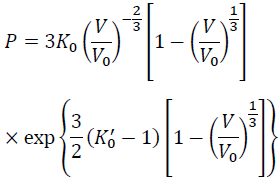
(6)
Comparison of these EOS's is discussed in a separate page.
The above EOS's are expressed using KT0 and K0'. The reason for these formulas is that these two parameters can be estimated by elastic wave velocity [Wiki] measurement. Although sometimes a higher order EOS, for example, 4th-order Birch-Murnaghan EOS is referred, it is impractical, because the 2nd P derivative of KT is extremely difficult to determine.
The main argument of EOS was made more than half century ago. At that time, pressure ranges of laboratory experiments were very limited (at best a couple of GPa). In those days, the Earth's structure should be estimated based on such experimental data obtained at such pressures. The 2nd-order Birch-Murnaghan EOS was some kind of miracle, because it can estimate density of minerals if one has a value of bulk modulus at ambient pressure. These days, the DAC can reach the pressure at the Earth's center, and density of Earth's constituents can be obtained directly. Therefore, argument about EOS has become much less important.
