Simplest EOS
KT,0 is the isothermal bulk modulus [Wiki] at zero P. Its definition is:
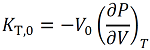
(1)
Then,
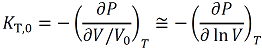
(2)
or more strictly,

(2')
By integrating Eq. (3), we have:
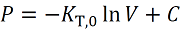
(3)
The integral constant C is determined from the condition that V = V0 at P = 0:
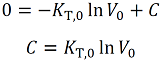
(4)
By substituting Eq. (4) into Eq. (3), we have:

(5)
Eq. (5) is the simplest EOS. However, it is not applicable for our interest, because materials become more incompressive due to compression, or with increasing P. Therefore, we need an EOS in which KT,0 increases with P.
It is noted that, although some literature shows a line for the simplest EOS in the V/V0 - P space, it is incorrect, as is seen from Eq. (5). The blue curve of Fig. 1 (below) shows the V/V0 against P by the simplest EOS. Of course, the intersection of the tangential line of the simplest EOS with the P axis shows KT,0.
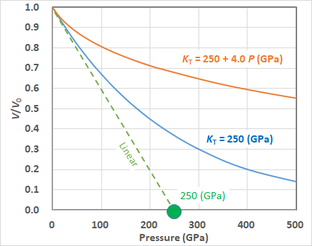
Fig. 1. The V/V0 - P relations by the simplest EOS (blue) and Murnaghan linear EOS (orange). Note that the relation by the simplest EOS is also curved and deviated from the
linear relation.
