Eulerian finite strain
When strains are infinitesimal, dimensions of objects are linearly decreased with P. However, this situation is not the case at high P. Matters become more incompressive with P. We therefore need a theory to treat this phenomenon, the finite strain theory [Wiki].
The general finite strain theory treats various kinds of large deformation. However, our present interest is how V decreases with P. In other words, it is how P increases with compression. This relation is called "equation of state" (EOS).
The most frequently used EOS is the third-order Birch-Murnaghan EOS. The base of this EOS is the Eulerian finite strain. In this page, the Eulerian finite strain is introduced as plainly as possible.
The following two points are essential for the Eulerian finite strain.
One is that compression is expressed not by a state before compression but by a state after compression as a reference. It is discussed how different these two ways are in a separate page.
The other is that we start discussion from change in squared length before and after compression. It is discussed in a separate page why the squared length is essential.
Let us consider a cube with an edge length of X0 and volume V0 = X03 in an unstrained state. This cube is uniformly compressed to an edge length of X and volume V = X3 (See the figure below). The change of the edge length is expressed by u.

Namely,

(1)

(2)

(3)
As is mentioned above, we argue change in squared edge lengths by compression. Namely,

(4)
The change in edge length, u, should be proportional to edge length itself. In the Eulerian strain theory, situations are expressed by the coordinates after compression. Accordingly, we relate the change in edge length from the edge length after compression, as follows:

(5)
Using Eq. (5), Eq. (4) becomes:

(6)
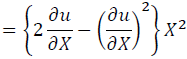
(7)
We then define the Eulerian finite strain as:

(8)
Note that Eq. (8) without the second term is identical to the infinite strain.
The difference of squared length is expressed using the Eulerian strain (Eq. 8) as:

(9)


(10)
Then, the ratio of the edge length before and after compression is expressed by the finite strain as:

The volume ratio is also expressed by the finite strain as:

(11)
From Eq. (12), we have

(12)
Then, the Eulerian strain is expressed by the volume ratio as:

(13)
The ε is negative when the cube is compressed. For convenience, we introduce f so that it is positive by compression.

(14)
Usually, f is called the finite strain in the field of high-pressure science.
The explanation in this page was constructed by referring to P. 66-69 in Poirier [2000]. In this book, the finite strain is first expressed by using tensor. However, it is unnecessary to do so, if we just want to understand compression at high pressures and Birch-Murnaghan EOS. I also suggest that, although Poirier [2000] expressed X0 , X and u in this page as dS and ds, and du, the expression by differential is not essential, because we consider uniform and finite compression.
Reference:
Poirier, J. P. Introduction to the physics of the Earth's Interior 2nd edition, Cambridge University Press, Cambridge, pp. 312, 2000.
